Проверочная работа ( тест) на 15 мин. Маятниковые часы спешат что нужно сделать чтобы они шли верно опустить
Механические колебания
24. Механические колебания.
24.1. Воронка с песком подвешена на нити. Будет ли изменяться период колебаний воронки по мере высыпания песка?
24.2. Груз на пружине колеблется в кабине лифта. Изменится ли период колебаний груза, если лифт начнет подниматься с ускорением?
24.3. Маятниковые часы немного спешат. Что нужно сделать чтобы они шли верно: опустить их в шахту или поднять на гору?
24.4. Вода, которую несут в ведре, начинает сильно расплескиваться. Как, не останавливаясь, прекратить расплескивание воды?
24.5. Груз массой m совершает колебания на вертикальной пружине жесткостью k. Являются ли эти колебания гармоническими и каков период их колебаний?
24.6. Груз массой m висит на пружине жесткостью k. В момент t = 0 грузу толчком сообщили скорость v вдоль оси пружины. Написать зависимости от времени: смещения x(t), скорости vx(t) и ускорения ax(t) груза.
24.7. Зная амплитуду A и максимальное значение скорости vmax, найти круговую частоту гармонических колебаний.
24.8. Зная амплитуду скорости vmax и амплитуду ускорения amах, найти амплитуду смещения и круговую частоту гармонических колебаний.
24.9. Какая была длина математического маятника, если при уменьшении его длины на 5 см частота колебаний увеличилась в 1,5 раза?
24.10. Один математический маятник имеет период колебаний 3 с, а другой – 4 с. Каков период колебаний маятника, длина которого равна сумме длин указанных маятников?
24.11. Какую часть периода груз маятника находится в пределах 1 см от положения равновесия, если амплитуда его колебаний равна 2 см?
2

Рис. 1
4.12.Во сколько раз время прохождения гармонически колеблющейся точкой первой половины амплитуды меньше времени прохождения второй половины амплитуды?24.13. Точка совершает гармонические колебания вдоль прямой. Зная, что максимальная скорость точки равна 10 м/с, найти среднюю скорость ее движения.
24.14. Математический маятник длиной l совершает колебания вблизи вертикальной стенки. Под точкой подвеса на расстоянии l/2 от нее в стену вбит гвоздь (рис. 1). Каков период колебаний маятника?
24.15. Брусок массой m совершает горизонтальные гармонические колебания с амплитудой A на пружине жесткости k. На расстоянии A/2 от положения равновесия установили массивную плиту, от которой брусок абсолютно упруго отскакивает. Каким стал период колебаний?
24.16. Груз висит на резинке. Может ли такая система совершать вертикальные гармонические колебания с амплитудой 2 см и частотой 5 Гц?
24.17. Груз массой M совершает вертикальные колебания на пружине жесткостью k с амплитудой A. Когда груз находился в крайнем нижнем положении, на него положили тело массой m, в результате чего колебания прекратились. Найти m.
24.18. Брусок массой M = 2 кг лежит на гладкой горизонтальной поверхности и соединен с вертикальной стенкой горизонтальной пружиной жесткости k = 2 Н/см. Пуля массой m = 10 г, летящая горизонтально вдоль пружины со скоростью v = 200 м/с, попадает в брусок и застревает в нем. Написать уравнение x(t) возникших колебаний. Положение равновесия принять за x = 0.
24.19. На гладкой горизонтальной поверхности находится брусок массой M, связанный с вертикальной стеной пружиной жесткости k. На бруске лежит второй брусок массой m. Систему отклоняют от положения равновесия и она начинает совершать гармонические колебания. При какой максимальной амплитуде колебаний они будут еще гармоническими, если коэффициент трения между брусками равен ?
2
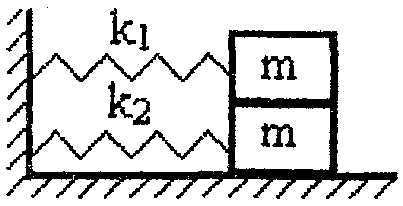
Рис. 2
Рис. 3
4.20. Два одинаковых бруска массойm каждый лежат один на другом и связаны пружинами жесткостью k1 и k2 с вертикальной стенкой (рис. 2). Система совершает горизонтальные колебания по гладкой горизонтальной поверхности. При какой максимальной амплитуде колебаний бруски еще не будут скользить друг по другу, если коэффициент трения между ними равен ? Положения равновесия для пружин совпадают.24.21. В представленной на рис. 3 системе период вертикальных колебаний тела равен T. Каким будет период колебаний, если систему перевернуть на 180° сверху вниз?
2

Рис. 4
4.22.Груз массой m висит на двух пружинах, жесткости которых равны k1 и k2. Пружины соединены: а) последовательно; б) параллельно (рис. 4). Каков период колебаний системы?24.23. От груза, висящего на пружине жесткости k, отваливается часть массой m. На какую максимальную высоту поднимется после этого оставшаяся часть груза?
24.24. Тело, висящее на пружине, имело период вертикальных колебаний T1. Когда массу тела изменили, период колебаний стал равен T2. На сколько сместилось при этом положение равновесия?
2
Рис. 5
4.25.Груз имеет массу m = 1 кг, а пружины – жесткость k = 2500 Н/м (рис. 5). Какой будет амплитуда колебаний груза, если его отклонить от положения равновесия на l = 3 см и сообщить ему скорость v = 2 м/с?24.26. Тело массой m1совершает горизонтальные гармонические колебания на пружине с амплитудой A1. Когда оно проходит положение равновесия, на него вертикально падает тело массой m2 и прилипает. Найти новую амплитуду колебаний.
24.27. Точка совершает гармонические колебания. При смещении точки от положения равновесия на x1 = 2,4 см ее скорость равна v1 = 3 см/с, а при смещении на x2 = 2,8 см скорость равна v2 = 2 см/с. Найти амплитуду и период колебаний точки.
24.28. Уравнения колебаний имеет вид: x(t) = Asin t. Известно, что при фазе колебания 1 = /6 смещение равно x1 = 2 см. Определить амплитуду колебаний и смещение при фазе 2 = 3/4.
24.29. Точка совершает гармонические колебания. В момент to = 0 координата точки равна xo = 25 см, а скорость – vo = 100 см/с. Определить координату и скорость точки в момент t = 2,4 с, если круговая частота колебаний равна = 4 с–1. В положении равновесия x = 0.
24.30. Точка совершает гармонические колебания по закону: x(t) = Asin t. В некоторый момент смещение точки от положения равновесия равно x1 = 5 см. При увеличении фазы колебаний вдвое смещение стало равно x2 = 8 см. Найти амплитуду колебаний.
24.31. Точка совершает гармонические колебания. При этом на расстояниях x1 и x2 от положения равновесия скорость точки равна v1 и v2. Определить амплитуду и круговую частоту колебаний точки.
24.32. Когда груз неподвижно висит на пружине он растягивает ее на 5 см. Каков период колебаний груза на этой пружине?
24.33. К динамометру подвесили груз. При этом возникли колебания с частотой 2 Гц. На каком расстоянии от нулевой отметки остановится указатель динамометра, когда колебания прекратятся?
24.34. Тело массой m совершает горизонтальные гармонические колебания на пружине жесткостью k с амплитудой A. Определить максимальную мощность, развиваемую силой упругости пружины.
24.35. Тело может совершать горизонтальные гармонические колебания на пружине. Тело отклонили от положения равновесия и отпустили. Найти отношение кинетической энергии системы k потенциальной через время t после начала колебаний, если их период равен T. Массой пружины пренебречь.
2

Рис. 6
4.36.Тело совершает гармонические колебания с периодом T. Через какой промежуток времени кинетическая и потенциальная энергии тела оказываются равными?24.37. Показать, что период обращения математического маятника по горизонтальной окружности (конический маятник), равен периоду его колебаний при малых углах отклонения.
24.38. Тело находится внутри сферы в некоторой точке A. В каком случае тело быстрее достигнет нижней точки сферы B: если оно будет скользить по сфере или по наклонной плоскости AB (рис. 6)? Трения нет, расстояние AB много меньше радиуса сферы.
24.39. Вообразим, что между двумя городами сквозь Землю прорыт прямолинейный тоннель, в котором проложены рельсы. Сколько времени будет двигаться вагон по этому тоннелю от одного города до другого, если его отпустить без начальной скорости? Трением и сопротивлением воздуха пренебречь.
2
Рис. 7
4.40. Два одинаковых горизонтальных цилиндрических валика быстро вращаются в противоположныхнаправлениях. Расстояние между осями валиков равно l. Навалики положили однородную доску, как показано на рис.7. Показать, что доска будет совершать гармоническиеколебания и найти их период, если коэффициент трениямежду доской и валиками равен .24.41. Поплавок переносят из жидкости с меньшей плотности в жидкость с большей плотностью. Как при этом изменяется период вертикальных колебаний поплавка?
24.42. В пробирку насыпали немногопеска и опустили ее плавать в воду (рис. 8). Какими будут вертикальные колебания пробирки? Найти их период. Масса пробирки равна m, площадь ее поперечного сечения – S.
2
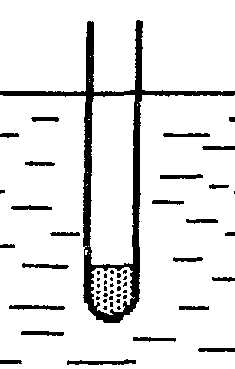
Рис. 8
4.43. Однородный цилиндр длинойl плавает в вертикальном положении на границе двух несмешивающихся жидкостей с плотностями 1 и 2 (1 < 2) и делится этой границей пополам. Пренебрегая сопротивлением, найти период малых вертикальных колебаний цилиндра.2
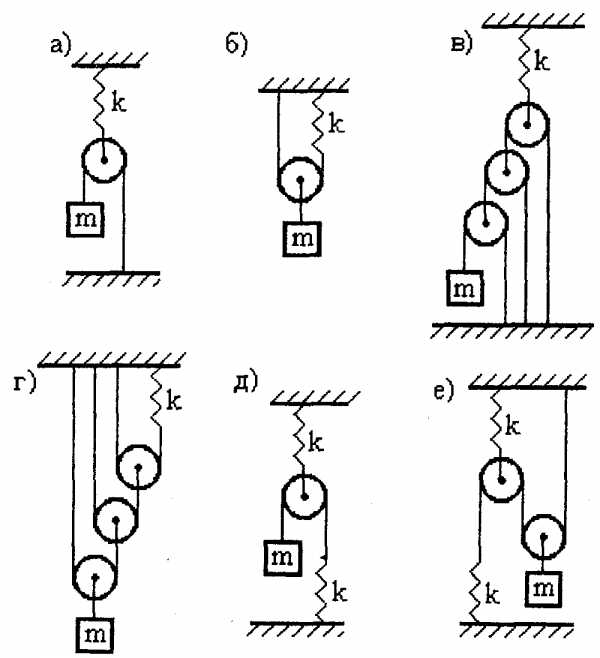
Рис. 9
4.44. Невесомая горизонтальная платформа стоит, как на ножках, на четырех одинаковых вертикальных пружинах. С высотыh в середину платформы падает кусочек пластилина массой m и прилипает к ней. Какова амплитуда возникших при этом колебаний? Жесткость каждой пружины равна k.24.45. Чашка массой M стоит на вертикальной пружине жесткости k. С высоты h в чашку падает пластилиновый шарик массой m и прилипает к ней. На какую максимальную высоту от начального положения опустится при этом чашка?
24.46. Определить период гармонических колебаний систем, изображенных на рис. 9 а) – е). Масса всех грузов равна m, жесткость всех пружин равна k. Пружины и блоки невесомые, нити невесомые и нерастяжимые, трения нет.
24.47. На груз массой M, висящий на пружине, кладут еще один груз массой m, удерживая систему в начальном положении. Затем грузы отпускают. Найти максимальную силу, действующую на верхний груз со стороны нижнего.
24.48. Тонкий обруч массой M и радиусом R может без трения вращаться вокруг горизонтальной оси, проходящей через центр обруча. На обруче закреплен небольшой грузик массой m. Найти период малых колебаний обруча.
24.49. Колебания описываются уравнением: x(t) = 3sin t + 4cos t (см). Являются ли эти колебания гармоническими и какова их амплитуда?
2

Рис. 10
4.50. Период вертикальных колебаний груза на резиновом шнуре равенT. Каким будет период колебаний этого груза на том же шнуре, сложенном вдвое?24.51. Небольшой шарик массой m совершает колебания с амплитудой A на нити длиной l (A << l). На сколько изменяется сила натяжения нити в процессе колебаний?
24.52. Математический маятник совершает малые колебания в вертикальной плоскости на нити длиной l. На расстоянии x под точкой подвеса торчит гвоздь, на который натыкается нить маятника (рис. 10). Определить отношение углов наибольших отклонений нити маятника от вертикали влево и вправо.
24.53. Найти период колебаний жидкости в U – образной трубке постоянного сечения, если общая длина трубки, заполненной жидкостью равна l.
2
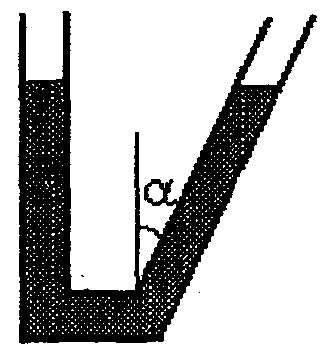
Рис. 11
4.54.Жидкость объемом V = 16 см3 налита в V – образную трубку с площадью сечения S = 0,5 см2. Одно колено трубки вертикально, а другое наклонено к вертикали под углом = 30° (рис. 11). Определить период колебаний жидкости в трубке. Вязкость не учитывать.24.55. Груз массой m = 0,25 кг лежит на гладкой горизонтальной поверхности между двумя пружинами, жесткость которых равна k1 = 150 Н/м и k2 = 250 Н/м. Первоначально пружины ненагружены. В некоторый момент конец пружины k2 резко сдвигают на расстояние a = 4 см в сторону груза и закрепляют. Определить амплитуду и максимальную скорость возникших колебаний.
2
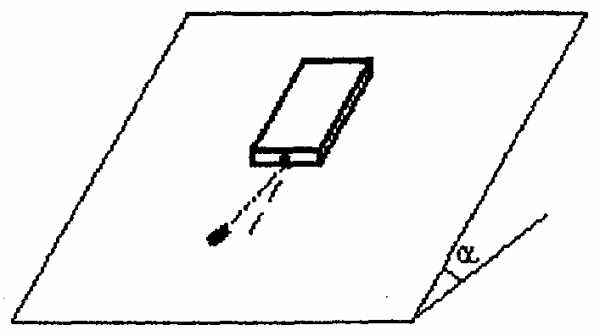
Рис. 12
4.56.На наклонной плоскости находится брусок, к которому на нити подвешена небольшая шайба. Шайба без трения совершает гармонические колебания с периодом To (рис. 12). Каким будет период колебаний шайбы, если брусок отпустить? Угол наклона плоскости равен , коэффициент трения между бруском и плоскостью равен , масса бруска намного больше массы шайбы.2
Рис. 13
4.57.Система состоит из двух брусков массами m и 2m, между которыми пружина жесткости k. Систему поставили вертикально (рис. 13). При какой максимальной амплитуде колебания верхнего бруска массой m будут гармоническими?2
Рис. 14
4.58.Два тела массой m каждое связаны пружиной жесткости k и движутся со скоростью v по гладкой горизонтальной поверхности к стенке. В некоторый момент одно из тел находилось на расстоянии L от стенки (рис. 14). Через какое время оно опять будет находиться на расстоянии L от стенки? Начальных колебаний нет, столкновения со стенкой абсолютно упругие.2
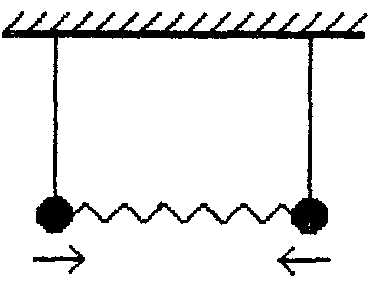
Рис. 15
4.59.Два одинаковых маленьких шарика массой m каждый висят на двух одинаковых вертикальных нитях длиной l и связаны пружиной жесткости k (рис. 15). Шарикам сообщили одинаковые небольшие скорости навстречу друг другу. Определить период возникших малых колебаний.24.60. Два грузика массами m1 и m2, связанные пружиной жесткости k, лежат на гладкой горизонтальной поверхности. Каков период колебаний такой системы?
24.61. На горизонтальной поверхности находится тележка массой M с установленным на ней математическим маятником массой m и длиной l. Каков период колебаний системы? Трения нет.
24.62. Во сколько раз частота колебаний молекулы h3 отличается от частоты колебаний молекулы DH?
2
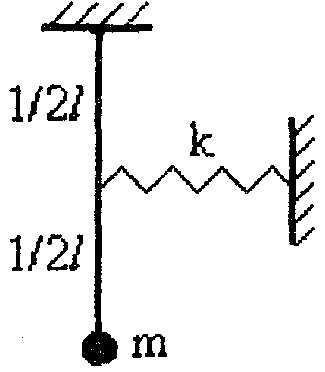
Рис. 16
4.63.Математический маятник установлен на тележке. Период колебаний маятника на неподвижной тележке равен To. Каким будет период колебаний, если тележка начнет скатываться без трения с наклонной плоскости с углом наклона ?2
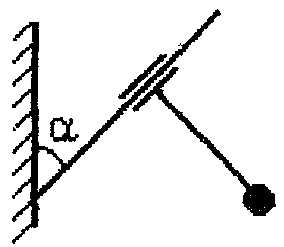
Рис. 17
4.64.В ракете установлены маятниковые часы. Ракета стартует вертикально вверх с ускорением 0,5g. На высоте h ракета начинает двигаться равнозамедленно с тем же ускорением. В момент старта часы в ракете показывали точное время. На какой высоте они опять будут показывать точное время? Изменением ускорения свободного падения с высотой пренебречь.24.65. Определить период колебаний системы (рис. 16).
24.66. Маятник представляет собой легкий жесткий стержень длиной l с грузом на конце. Стержень может вращаться вокруг оси, наклоненной к вертикали под углом (рис. 17). Определить период колебаний маятника.
2
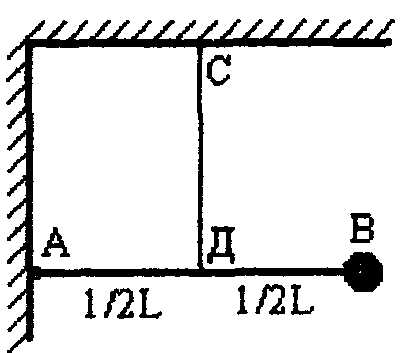
Рис. 18
Рис. 19
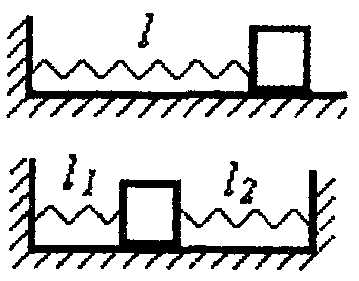
Рис. 20
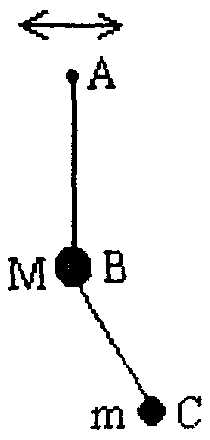
Рис. 21
4.67.Легкий стержень AB прикреплен шарнирно к стене и удерживается горизонтально вертикальной нитью CD длиной l. На конце стержня укреплен небольшой массивный шарик (рис. 14.18). Найти период малых колебаний системы.24.68. Колебательная система представляет собой легкий стержень, на концах которого закреплены маленькие шарики массами m1 и m2. Стержень может без трения вращаться вокруг горизонтальной оси O, находящейся на расстояниях l1 и l2 от шариков (рис. 19). Найти период малых колебаний системы.
24.69. Невесомый стержень длиной l шарнирно подвешен к потолку. На конце и в середине стержня укреплены два одинаковых маленьких массивных шарика. Определить период малых колебаний стержня.
24.70. Груз, лежащий на гладкой горизонтальной поверхности, прикреплен пружиной длиной l к вертикальной стене. Пружину разрезали на две части длиной l1 и l2 и соединили их с тем же грузом между двумя стенками (рис. 20). Найти период горизонтальных колебаний груза во втором случае, если в первом случае период был равен To.
24.71. К маятнику AB с шариком массой M подвешен маятник BC с шариком массой m. Точка A совершает горизонтальные колебания с периодом T (рис. 21). Найти длину нити BC, если нить AB все время остается вертикальной.
24.72. Математический маятник совершает малые колебания с угловой амплитудой . Скорость груза в нижней точке равна v. В крайнем положении грузу толчком сообщают скорость v в направлении перпендикулярном плоскости колебаний. По какой траектории будет двигаться груз? Через какое время онопять попадет в ту же точку?
24.73. Точка совершает движение в плоскости x, y по закону: x(t) = Asin t; y(t) = Acos t. Что является траекторией движения точки? Определить ускорение точки.
24.74. Частица колеблется вдоль оси x по закону: x(t) = Acos t. Построить графики зависимости скорости частицы и ее ускорения от координаты: v(x) и a(x).
24.75. Материальная точка движется в плоскости x, y по закону: x(t) = Asin t; y(t) = Acos 2t. Что является траекторией движения точки?
24.76. Полый шар заполнен водой и совершает колебания на нити. Как изменится период колебаний, если вода замерзнет? Изменение объема при замерзании не учитывать.
24.77. Твердое тело совершает малые колебания вокруг горизонтальной оси с периодом To. Каким будет период колебаний тела, если при неизменной плотности все его линейные размеры увеличатся вдвое?
24.78. Правильно идущие механические часы положили на гладкую горизонтальную поверхность. Как изменится темп хода часов?
24.79. Однородный стержень массой m и длиной l, шарнирно подвешенный за один конец, совершает малые колебания с угловой амплитудой . Чему равны период и полная энергия колебаний стержня? Трения нет.
24.80. Тело может без трения вращаться вокруг горизонтальной оси. Тело расположили так, что его центр масс оказался точно над осью и отпустили без начальной скорости. При этом тело прошло положение равновесия с угловой скоростью . Найти период малых колебаний тела.
2
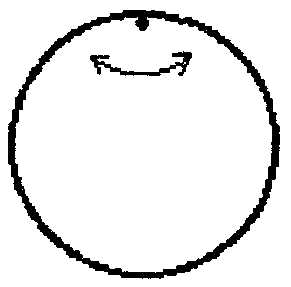
Рис. 22
4.81.Два тела совершают малые колебания вокруг одной и той же оси с круговыми частотами 1 и 2. Моменты инерции тел относительно этой оси равны J1 и J2 соответственно. С какой частотой будут колебаться тела, если их соединить вместе?24.82. Однородный тонкий стержень колеблется вокруг горизонтальной оси, проходящей через стержень и отстоящей от одного из его концов на расстояние x. При каком значении x период колебаний стержня будет наименьшим, если длина стержня равна L. Трения нет, колебания малые.
2
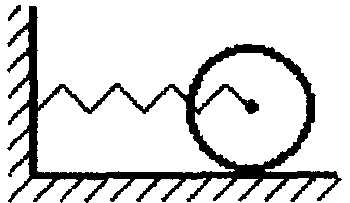
Рис. 23
4.83.Тонкий обруч радиусом R повесили на вбитый в стену гвоздь (рис. 22). Найти период малых колебаний обруча. Проскальзывания нет.24.84. Однородный цилиндр массой m и радиусом R колеблется на пружине жесткости k в горизонтальной плоскости (рис. 23). Найти период колебаний, если цилиндр не проскальзывает. При какой амплитуде колебаний начинается проскальзывание цилиндра, если коэффициент трения между цилиндром и плоскостью равен ?
2
Рис. 24
4.85.Однородный цилиндр радиусом r катается по внутренней поверхности цилиндра радиусом R (рис. 24). Найти период малых колебаний. Проскальзывания нет.2

Рис. 25
4.86.Однородный стержень, висящий на двух одинаковых вертикальных нитях длиной l, повернули на малый угол вокруг вертикальной оси, проходящей через его центр, и отпустили (рис. 25). Каков период малых колебаний стержня?24.87. Длинный поезд, движущийся по инерции по горизонтальному пути, начинает въезжать в гору с углом наклона . Через какое время поезд остановится? Длина поезда L, трения нет. Известно, что поезд въехал в гору только частично.
2
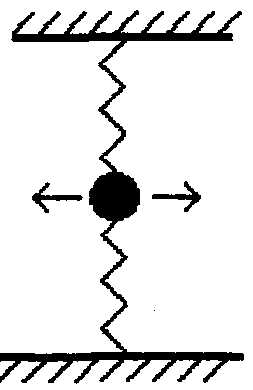
Рис. 26
4.88.Доска длиной L скользит без трения по льду вдоль своей длины и въезжает на асфальтированный участок. Через какое время доска остановится, если коэффициент трения между доской и асфальтом равен . Известно, что доска въезжает на асфальт лишь частично.24.89. Частица массой m находится в силовом поле, где ее потенциальная энергия зависит от координаты по закону: W(x) = Wo(l – cos x). Найти период малых колебаний частицы около положения равновесия.
24.90. Система, показанная на рис. 26, совершает колебания перпендикулярно пружинам. Возможны ли гармонические колебания такой системы? Пружины одинаковы и в положении равновесия нерастянуты. Внешних сил нет.
Ответы, указания.
1. Не будет.
2. Не изменится.
3. Поднять в гору.
4. Сменить темп хода.
5. Являются;  .
.
6. ,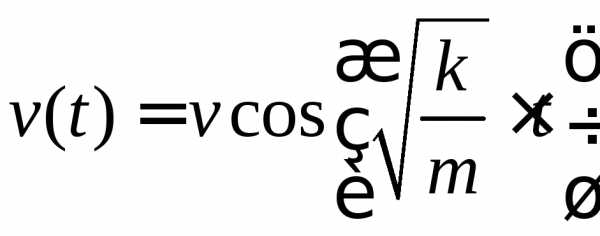 ,.
,.
7. 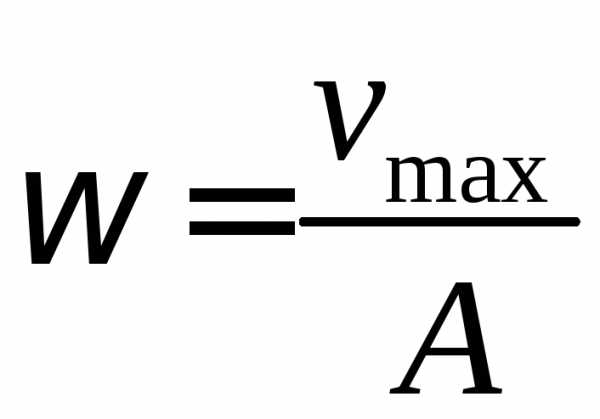 .
.
8. 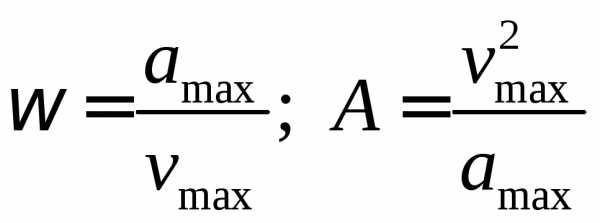 .
.
9. 9 см.
10. 5 с.
11. 1/3.
12. 2.
13. 6,4 см.
14. 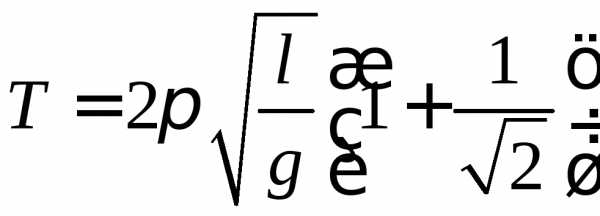 .
.
15.  .
.
16. Не может.
17.  .
.
18. .
19.  .
.
20.  .
.
21. T.
22. а) ;б)
;б)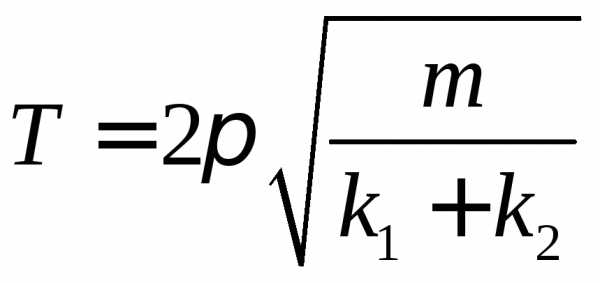 .
.
23. 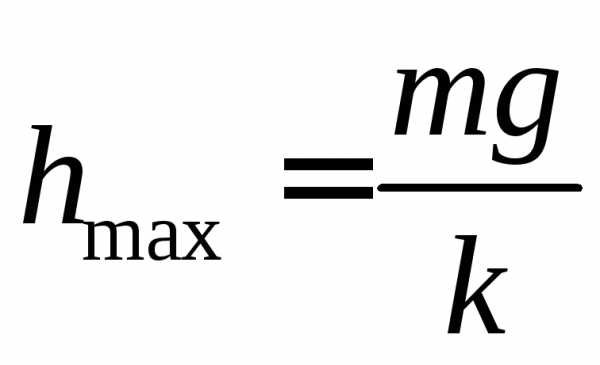 .
.
24.  .
.
25. 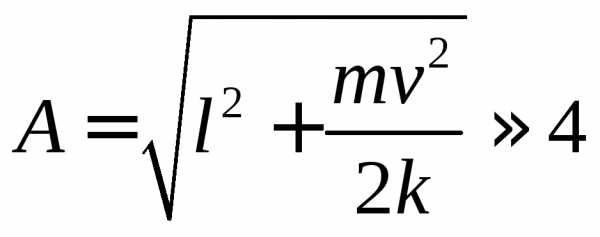 см.
см.
26.  .
.
27. см; .
.
28. 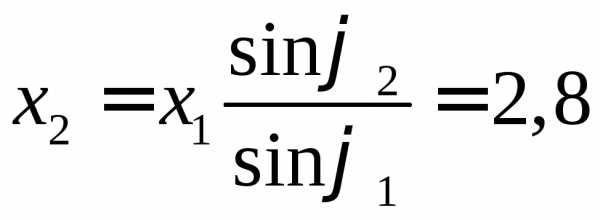 см.
см.
29. см;
см/с.
30. 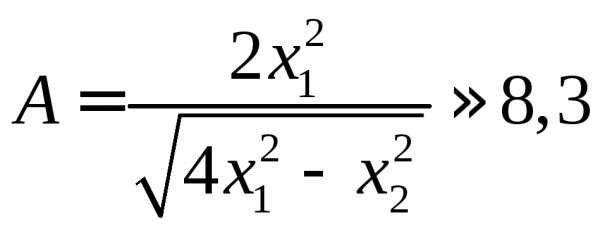 см.
см.
31. .
32. 0,45 с.
33. 6,3 см
34.  .
.
35. 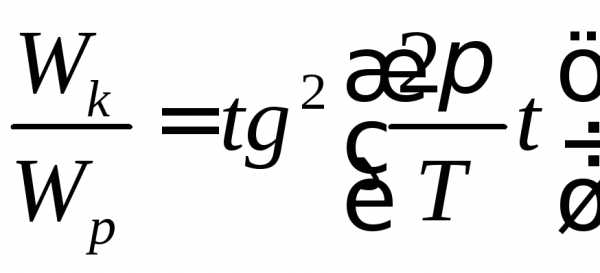 .
.
36.  .
.
38. По сфере быстрее.
39. 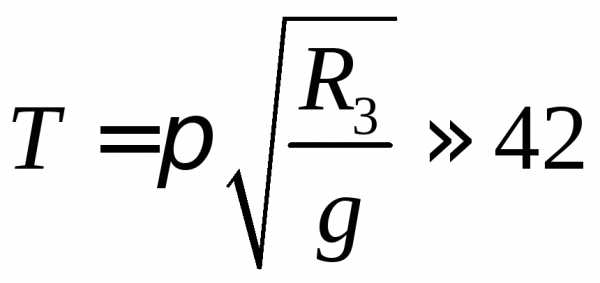 мин.
мин.
У
Рис.
казание: Второй закон Ньютона:, где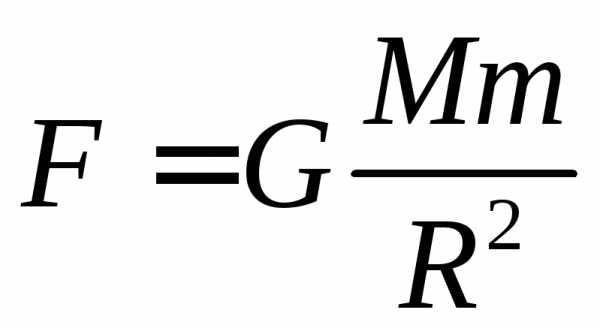 – сила тяжести, действующая на тележку в тоннеле (
– сила тяжести, действующая на тележку в тоннеле ( , где– средняя плотность Земли). Отклонение тележки от положения равновесия(рис.). Отсюда получаем:– уравнение гармонических колебаний.
, где– средняя плотность Земли). Отклонение тележки от положения равновесия(рис.). Отсюда получаем:– уравнение гармонических колебаний. 40.  .
.
Указание: Если центр доски совпадает с серединой расстояния между центрами цилиндров, то силы давления доски на цилиндры будут разные, а, значит, разными будут и силы трения, действующие на доску со стороны цилиндров. Если связать ускорение доски с величиной смещения центра доски от средней точки, то получится уравнение гармонических колебаний.
studfiles.net
Проверочная работа ( тест) на 15 мин - Урок
Тема: Фаза колебаний. ( 11 класс )
Цель урока: Ввести характеристику гармонических колебаний – фаза колебаний, расширив при этом представление учащихся о гармонических колебаниях.
Выяснить физический смысл понятий: “фаза колебания”, “начальная фаза”, “сдвиг фаз”.
Демонстрации:
Пружинный и математический маятники.
Осциллограф.
Применение интерактивной доски для показа гармонических колебаний.
Слайд- шоу.
Ход урока:
Проверка знаний. Проверочная работа ( тест) на 15 мин.
Вариант 1.
Маятник совершает колебания с частотой 10 Гц. Определите циклическую частоту.
А. 6,26 Гц. Б. 0,5 ПГц. В. 62,8 Гц.
Как изменится период колебаний математического маятника, если его длину увеличить в 9 раз?
А. Увеличится в 9 раз. Б. Увеличится в 3 раза. В. Уменьшится в 3 раза.
3. Груз на пружине совершает колебания. Коэффициент жесткости равен 100Н/м. При смещении груза на 5 см его ускорение равно 0,5 м/с2. Какова масса груза?
А. 10 кг. Б. 1 кг. В. 5 кг.
4. Период колебаний пружинного маятника на Земле равен 1 с. Как изменится период колебаний этого маятника на Луне?
А. Не изменится. Б. Возрастет. В.Уменьшится.
5. Как изменится период колебания математического маятника, если амплитуда увеличится?
А. Не изменится. Б. Возрастет. В. Уменьшится.
6. Как изменится период колебания математического маятника в вертолете, который поднимается с ускорением, направленным вертикально вверх?
А. Уменьшится. Б. Не изменится. В. Увеличится.
7. Изменится ли период колебания математического маятника обтекаемой формы при опускании его в воду? (Трением пренебречь.)
А. Уменьшится. Б. Не изменится. В. Увеличится.
8. Сохранится ли частота колебаний шарика, закрепленного на пружине, если вся система окажется в состоянии невесомости?
А. Сохранится. Б. Увеличится. В. Уменьшится.
9. Какими часами следует измерять время в условиях невесомости?
А. Маятниковыми. Б. Песочными. В. Пружинными.
10. Во сколько раз надо изменить длину математического маятника, чтобы период колебания изменился в 2 раза ? А. Не изменится. Б. Изменится в 4 раза. В.Изменится в 2 раза.
Вариант 2.
Маятник совершает колебания с периодом 2 с. Определите циклическую частоту.
А. 3,14 с-1. Б. 4 Пс-1. В. 12.56 с-1.
2. Каков период колебания математического маятника длиной 0.4 м?
А. 4 Пс. Б.0,02 Пс. В.0,4 Пс.
3. Как изменится модуль ускорения груза, колеблющегося на пружине, если смещение увеличится в 4 раза?
А. Уменьшится в 4 раза. Б. Увеличится в 2 раза. В. Увеличится в 4 раза.
4. Пружина имеет постоянную жесткость, равную 10 Н/м. Масса груза равна 100 г. Какую массу нужно подвесить к этой пружине, чтобы период колебания уменьшился в 2 раза?
А. 25 г. Б. 50 г. В. 200 г.
5. Груз подвешен на длинной нити. Как изменится период его колебания, если массу груза увеличить?
А. Увеличится. Б. Уменьшится. В. Не изменится.
6. Как изменится период колебания маятника на пружине в вертолете, движущемся с ускорением, направленным вертикально вниз?
А. Не изменится. Б. Увеличится. В. Уменьшится.
7. Маятниковые часы спешат. Что нужно сделать, чтобы они шли верно: опустить их в шахту или поднять на определенную высоту?
А. Опустить. Б. Поднять на определенную высоту.
8. Как изменится частота колебаний железного шарика, подвешенного на нити, если под ним поместить электромагнит?
А. Не изменится. Б. Увеличится. В. Уменьшится.
9. В условиях невесомости было использовано устройство для измерения массы космонавта – массометр, представляющий собой небольшую платформу на пружинах. Действие такого массометра основано на принципе измерения:
А.Амплитуды. Б. Скорости или ускорения В. Периода или частоты.
10. С помощью какого маятника: а) математического; б) пружинного – можно практически осуществить разведку полезных ископаемых?
А. а. Б. б. В. а
Ответы:
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
1 | В | Б | А | А | А | А | В | А | В | Б |
2 | А | В | В | А | В | А | Б | Б | В | А |
II. Изучение нового материала.
Фаза колебаний. ( Слайд 1 ).
Фаза колебаний φ – физическая величина, стоящая под знаком косинуса или синуса, описываемая этой функцией. От греческого слова phasis – появление, ступень развития какого – либо явления.
Выражается фаза в угловых единицах – радианах. Фаза определяет значение координаты, скорости, ускорения, изменяющихся также по гармоническому закону. Фаза определяет при заданной амплитуде состояния колебательной системы в любой момент времени.
φ═ωt.
Время в долях период/а Фаза в радианах
0 0
¼ T π/2
½ T π
¾ T 3/2 π
T 2π
Начальная фаза. (Слайд 2).
Фаза - это величина, которая характеризует состояние колеблющегося тела в некоторый момент времени - его положение и направление движения.
x = xmcos(wt+ φ0),
где xm– амплитуда, φ0 - начальная фаза колебаний в начальный момент времени (t =0), определяет положение колеблющейся точки в начальный момент времени.
3. Сдвиг фаз. Способы определения разности фаз ( графический и алгебраический ).(Слайд 3).
Разность фаз, или, как часто говорят, сдвиг фаз, этих колебаний составляет π /2. На слайде 3 показаны графики зависимости координат от времени для двух гармонических колебаний, сдвинутых по фазе на π /2. График 1 соответствует колебаниям, совершающимся по синусоидальному закону: x = xmsinω0t, а график 2 – колебаниям, совершающимся по закону косинуса x = xmsin(ω0t + π /2) = xmcosω0t.
Для определения разности фаз двух колебаний надо в обоих случаях колеблющуюся величину выразить через одну и ту же тригонометрическую функцию – косинус или синус.
Закрепление знаний, умений, навыков.
Фаза колебания равна π /2 ( 25π ). Охарактеризуйте колебательный процесс при этих значениях.
Определите смещение точки в гармоническом колебании спустя 0.25 периода после начала колебаний. Начальная фаза колебаний равна π /2.
Домашнее задание: § 23, вопросы.
Тема: Строение и свойства кристаллических и аморфных тел. (10 класс).
Цель урока: Рассмотреть особенности строения и свойства кристаллических и аморфных тел.
Демонстрации:
Набор кристаллических тел.
Набор моделей кристаллических решеток.
Применение интерактивной доски.
Слайд – шоу.
Ход урока:
I. Изучение нового материала.
Твердые тела.
Свойства твердых тел.
Кристаллические тела.
Анизотропия кристаллов.
Монокристаллы и поликристаллы.
Свойства кристаллов.
Аморфные тела.
Свойства аморфных тел.
Применение кристаллов.
Твердые тела – это тела, находящиеся преимущественно в кристаллическом состоянии.
Большинство окружающих нас тел – вещества в твердом состоянии. Специальная область физики занимается изучением строения и свойств твердых тел. “Физика твердого тела”- эта область физики является ведущей во всех физических исследованиях. В любой отрасли техники используются свойства твердого тела: механические, электрические, оптические и т. д. Все большее применение в технике находят кристаллы.
Вещества называют твердыми, если они сохраняют свою форму и объем, т. е. внешние признаки.
Кристаллы – это твердые тела, атомы или молекулы которых занимают определенные, упорядоченные положения в пространстве. Однако правильная внешняя форма не самое главное следствие упорядоченного строения кристалла. Главное – это зависимость физических свойств от выбранного в кристалле направления. Зависимость физических свойств от направления внутри кристалла называют анизотропией. ( От греческих слов «анизос» - неравный, «тропос» - направление ).(Слайд 2-6)
Кристаллические тела
Монокристаллы - Поликристаллы –
Одиночные кристаллы тела состоящие из большого числа
(кварц, алмаз ). маленьких кристалликов (металлы, сахар).
Свойства:
Температура плавления const.
Каждое вещество имеет свою температуру плавления. (Слайд 7).
Анизотропия – зависимость физических свойств от направления внутри кристалла.
Изотропия – одинаковые физические свойства по всем направлениям.
Аморфные тела (от греческого «морфе» - форма и частица «а», имеющий смысл отрицания ) занимают промежуточное положение между кристаллическими твердыми телами и жидкостями. (Слайд 8-11)
uchebana5.ru
24.1 Механические колебания: задачи с ответами без решений
(Все задачи по механическим колебаниям и ответы к ним находятся в zip-архиве (225 кб), который можно скачать и открыть на своем компьютере. Попробуйте решать задачи самостоятельно и только потом сравнивать свои ответы с нашими. Желаем успехов!)24.1. Воронка с песком подвешена на нити. Будет ли изменяться период колебаний воронки по мере высыпания песка? [смотрите ответ в общем файле]
24.2. Груз на пружине колеблется в кабине лифта. Изменится ли период колебаний груза, если лифт начнет подниматься с ускорением? [смотрите ответ в общем файле]
24.3. Маятниковые часы немного спешат. Что нужно сделать чтобы они шли верно: опустить их в шахту или поднять на гору? [смотрите ответ в общем файле]
24.4. Вода, которую несут в ведре, начинает сильно расплескиваться. Как, не останавливаясь, прекратить расплескивание воды? [смотрите ответ в общем файле]
24.5. Груз массой m совершает колебания на вертикальной пружине жесткостью k. Являются ли эти колебания гармоническими и каков период их колебаний? [смотрите ответ в общем файле]
24.6. Груз массой m висит на пружине жесткостью k. В момент t = 0 грузу толчком сообщили скорость v вдоль оси пружины. Написать зависимости от времени: смещения x(t), скорости vx(t) и ускорения ax(t) груза. [смотрите ответ в общем файле]
24.7. Зная амплитуду A и максимальное значение скорости vmax, найти круговую частоту гармонических колебаний. [смотрите ответ в общем файле]
24.8. Зная амплитуду скорости vmax и амплитуду ускорения amах, найти амплитуду смещения и круговую частоту гармонических колебаний. [смотрите ответ в общем файле]
24.9. Какая была длина математического маятника, если при уменьшении его длины на 5 см частота колебаний увеличилась в 1,5 раза? [9 см]
24.10. Один математический маятник имеет период колебаний 3 с, а другой — 4 с. Каков период колебаний маятника, длина которого равна сумме длин указанных маятников? [5 см]
24.11. Какую часть периода груз маятника находится в пределах 1 см от положения равновесия, если амплитуда его колебаний равна 2 см? [1/3]
24.12. Во сколько раз время прохождения гармонически колеблющейся точкой первой половины амплитуды меньше времени прохождения второй половины амплитуды? [2]
24.13. Точка совершает гармонические колебания вдоль прямой. Зная, что максимальная скорость точки равна 10 м/с, найти среднюю скорость ее движения. [≅ 6.4 см]
24.14. Математический маятник длиной l совершает колебания вблизи вертикальной стенки. Под точкой подвеса на расстоянии l/2 от нее в стену вбит гвоздь (рис. слева). Каков период колебаний маятника? [смотрите ответ в общем файле]
24.15. Брусок массой m совершает горизонтальные гармонические колебания с амплитудой A на пружине жесткости k. На расстоянии A/2 от положения равновесия установили массивную плиту, от которой брусок абсолютно упруго отскакивает. Каким стал период колебаний? [смотрите ответ в общем файле]
24.16. Груз висит на резинке. Может ли такая система совершать вертикальные гармонические колебания с амплитудой 2 см и частотой 5 Гц? [смотрите ответ в общем файле]
24.17. Груз массой M совершает вертикальные колебания на пружине жесткостью k с амплитудой A. Когда груз находился в крайнем нижнем положении, на него положили тело массой m, в результате чего колебания прекратились. Найти m. [смотрите ответ в общем файле]
24.18. Брусок массой M = 2 кг лежит на гладкой горизонтальной поверхности и соединен с вертикальной стенкой горизонтальной пружиной жесткости k = 2 Н/см. Пуля массой m = 10 г, летящая горизонтально вдоль пружины со скоростью v = 200 м/с, попадает в брусок и застревает в нем. Написать уравнение x(t) возникших колебаний. Положение равновесия принять за x = 0. [≅ 0.1sin (10t). Формула в общем файле]
24.19. На гладкой горизонтальной поверхности находится брусок массой M, связанный с вертикальной стеной пружиной жесткости k. На бруске лежит второй брусок массой m. Систему отклоняют от положения равновесия и она начинает совершать гармонические колебания. При какой максимальной амплитуде колебаний они будут еще гармоническими, если коэффициент трения между брусками равен μ? [смотрите ответ в общем файле]
24.20. Два одинаковых бруска массой m каждый лежат один на другом и связаны пружинами жесткостью k1 и k2 с вертикальной стенкой (рис. слева). Система совершает горизонтальные колебания по гладкой горизонтальной поверхности. При какой максимальной амплитуде колебаний бруски еще не будут скользить друг по другу, если коэффициент трения между ними равен μ? Положения равновесия для пружин совпадают. [смотрите ответ в общем файле]
24.21. В представленной на рис. слева системе период вертикальных колебаний тела равен T. Каким будет период колебаний, если систему перевернуть на 180° сверху вниз? [смотрите ответ в общем файле]
24.22. Груз массой m висит на двух пружинах, жесткости которых равны k1 и k2. Пружины соединены: а) последовательно; б) параллельно (рис. слева). Каков период колебаний системы? [смотрите ответ в общем файле]
24.23. От груза, висящего на пружине жесткости k, отваливается часть массой m. На какую максимальную высоту поднимется после этого оставшаяся часть груза? [смотрите ответ в общем файле]
24.24. Тело, висящее на пружине, имело период вертикальных колебаний T1. Когда массу тела изменили, период колебаний стал равен T2. На сколько сместилось при этом положение равновесия? [смотрите ответ в общем файле]
24.25. Груз имеет массу m = 1 кг, а пружины — жесткость k = 2500 Н/м (рис. слева). Какой будет амплитуда колебаний груза, если его отклонить от положения равновесия на l = 3 см и сообщить ему скорость v = 2 м/с? [≅ 4 см]
24.26. Тело массой m1 совершает горизонтальные гармонические колебания на пружине с амплитудой A1. Когда оно проходит положение равновесия, на него вертикально падает тело массой m2 и прилипает. Найти новую амплитуду колебаний. [смотрите ответ в общем файле]
24.27. Точка совершает гармонические колебания. При смещении точки от положения равновесия на x1 = 2,4 см ее скорость равна v1 = 3 см/с, а при смещении на x2 = 2,8 см скорость равна v2 = 2 см/с. Найти амплитуду и период колебаний точки. [ A ≅ 3.1 см; T ≅ 4.1 см; формулы в общем файле темы]
24.28. Уравнения колебаний имеет вид: x(t) = Asin (wt). Известно, что при фазе колебания φ1 = π/6 смещение равно x1 = 2 см. Определить амплитуду колебаний и смещение при фазе φ2 = 3π/4. [2.8 см, формула в общем файле]
24.29. Точка совершает гармонические колебания. В момент to = 0 координата точки равна xo = 25 см, а скорость — vo = 100 см/с. Определить координату и скорость точки в момент t = 2,4 с, если круговая частота колебаний равна w = 4 с−1. В положении равновесия x = 0. [смотрите ответ в общем файле]
24.30. Точка совершает гармонические колебания по закону: x(t) = Asin (wt). В некоторый момент смещение точки от положения равновесия равно x1 = 5 см. При увеличении фазы колебаний вдвое смещение стало равно x2 = 8 см. Найти амплитуду колебаний. [ A ≅ 8.3 см ]
Далее: следующие 30 задач по механическим колебаниям. | Вернуться в раздел МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ.
www.afportal.ru